请问小明今年几岁？首先我们设它为X，再根据勾股定理，物种起源，大陆漂移，修辞手法，过去式，现在进行时，圆周率推算，蝴蝶效应，阿基米德中点定理，阿基米德折弦定理，波尔查诺-维尔斯特拉斯定理，巴拿赫-塔斯基悖论伯特兰-切比雪夫定理，贝亚蒂定理，贝叶斯定理，博特周期性定理，闭图像定理，伯恩斯坦定理，康托尔-伯恩斯坦-施罗德定理，不动点定理，布利安桑定理，布朗定理，贝祖定理，博苏克-乌拉姆定理，半角定理，垂径定理，陈氏定理，采样定理，抽屉原理，D德摩根定律迪尼定理，等周定理，代数基本定理，多项式余数定理，大数定律，狄利克雷定理，棣美弗定理。
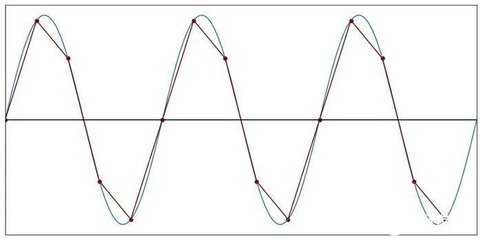1、采样定理怎么理解?
。在进行模拟/数字信号的转换过程中，当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>2fmax)，采样之后的数字信号完整地保留了原始信号中的信息，一般实际应用中保证采样频率为信号最高频率的5～10倍；采样定理又称奈奎斯特定理。
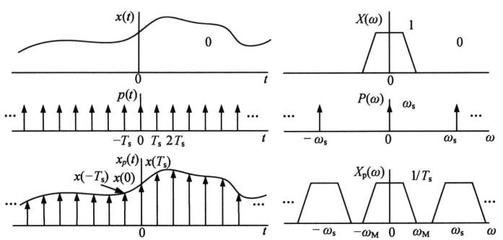2、采样定理
根据上节的讨论，如果连续时间信号的频谱分量的最高频率Ωc超过Ωs/2，那么各周期延拓分量在频率轴上将发生频谱的混叠现象。换句话说，为了使采样后的样本能够不失真的重构原始信号，那么采样频率必须大于两倍于原始信号频谱的最高频率物探数字信号分析与处理技术将1/2Ωs称为折叠频率，或尼奎斯特频率，记为ΩN，Ωc是信号频谱的最高频率。
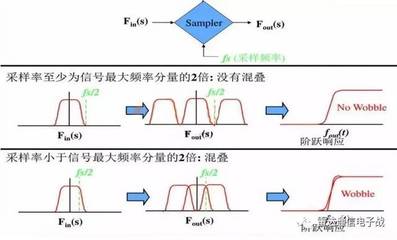3、为什么要用时域采样定理?
时域采样定理是采样误差理论、随机变量采样理论和多变量采样理论的基础。频带为F的连续信号f(t)可用一系列离散的采样值f(t1)，f(t1±Δt)，f(t1±2Δt)，…来表示，只要这些采样点的时间间隔Δt≤1/(2F)，便可根据各采样值完全恢复原来的信号f(t)。这是时域采样定理的一种表述方式。时域采样定理的另一种表述方式是：当时间信号函数f(t)的最高频率分量为fM时，f(t)的值可由一系列采样间隔小于或等于1/(2fM)的采样值来确定,
扩展资料：时域是真实世界，是惟一实际存在的域。因为人们的经历都是在时域中发展和验证的，已经习惯于事件按时间的先后顺序地发生，而评估数字产品的性能时，通常在时域中进行分析，因为产品的性能最终就是在时域中测量的。若考虑离散时间，时域中的函数或信号，在各个离散时间点的数值均为已知，若考虑连续时间，则函数或信号在任意时间的数值均为已知。